Hamiltonian Path is a path in a directed or undirected graph that visits each vertex exactly once. The problem to check whether a graph (directed or undirected) contains a Hamiltonian Path is NP-complete, so is the problem of finding all the Hamiltonian Paths in a graph. Following images explains the idea behind Hamiltonian Path more clearly.
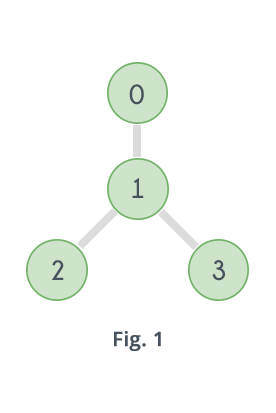
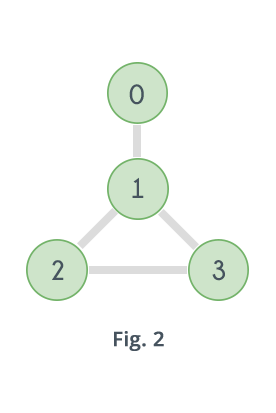
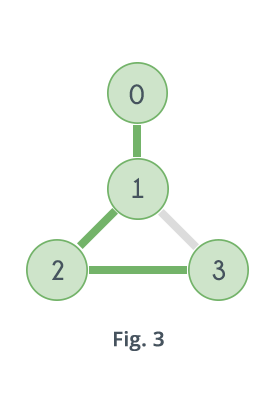
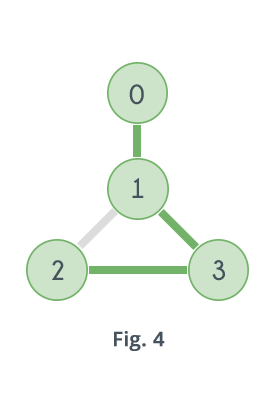
Graph shown in Fig.1 does not contain any Hamiltonian Path. Graph shown in Fig. 2 contains two Hamiltonian Paths which are highlighted in Fig. 3 and Fig. 4
Following are some ways of checking whether a graph contains a Hamiltonian Path or not.
-
A Hamiltonian Path in a graph having N vertices is nothing but a permutation of the vertices of the graph [v1, v2, v3, ......vN-1, vN] , such that there is an edge between vi and vi+1 where 1 ≤ i ≤ N-1. So it can be checked for all permutations of the vertices whether any of them represents a Hamiltonian Path or not. For example, for the graph given in Fig. 2 there are 4 vertices, which means total 24 possible permutations, out of which only following represents a Hamiltonian Path.
0-1-2-3
3-2-1-0
0-1-3-2
2-3-1-0
Following is the pseudo code of the above algorithm:function check_all_permutations(adj[][], n) for i = 0 to n p[i]=i while next permutation is possible valid = true for i = 0 to n-1 if adj[p[i]][p[i+1]] == false valid = false break if valid == true return true p = get_next_permutation(p) return false
The function get_next_permutation(p) generates the lexicographically next greater permutation than p.
Following is the C++ implementation:
bool check_all_permutations(bool adj[][MAXN], int n){ vector<int>v; for(int i=0; i<n; i++) v.push_back(i); do{ bool valid=true; for(int i=0; i<v.size()-1; i++){ if(adj[v[i]][v[i+1]] == false){ valid=false; break; }
} if(valid) return true; }while(next_permutation(v.begin(), v.end())); return false; }
Time complexity of the above method can be easily derived. For a graph having N vertices it visits all the permutations of the vertices, i.e. N! iterations and in each of those iterations it traverses the permutation to see if adjacent vertices are connected or not i.e N iterations, so the complexity is O( N * N! ). -
There is one algorithm given by Bellman, Held, and Karp which uses dynamic programming to check whether a Hamiltonian Path exists in a graph or not. Here's the idea, for every subset S
of vertices check whether there is a path that visits "EACH and ONLY" the vertices
in S exactly once and ends at a vertex v. Do this for all v S. A path exists that visits each vertex in subset S and
ends at vertex v S iff v has a neighbor w in S and
there is a path that visits each vertex in set S-{v} exactly once and ends
at w. If there is such a path, then adding the edge w-v to it will extend it to visit v and as it is already visiting every vertex in S-{v}, so the new path will visit every vertex in S.
For example, consider the graph given in Fig. 2, let S={0, 1, 2} and v=2. Clearly 2 has a neighbor in the set i.e. 1. A path exists that visits 0, 1, and 2 exactly once and ends at 2, if there is a path that visits each vertex in the set (S-{2})={0, 1} exactly once and ends at 1. Well yes, there exists such a path i.e. 0-1, and adding the edge 1-2 to it will make the new path look like 0-1-2. So there is a path that visits 0, 1 and 2 exactly once and ends at 2. Following is the pseudo code for the above algorithm, it uses bitmasking to represent subsets ( Learn about bitmasking here):
Let's try to understand it. The cell dp[j][i] checks if there is a path that visits each vertex in subset represented by mask i and ends at vertex j. In the first 3 lines every cell of table dp is initialized as false and in the following two lines the cells (i, 2i), 0 ≤ i < n are initialized as true. In the binary conversion of 2i only ith bit is 1. That means 2i represents a subset containing only the vertex i. And so the cell dp[i][2i] represents whether there is a path that visits the vertex i exactly once and ends at vertex i. And ofcourse for every vertex it should be true.function check_using_dp(adj[][], n) for i = 0 to 2n for j = 0 to n dp[j][i] = false for i = 0 to n dp[i][2i] = true for i = 0 to 2n for j = 0 to n if jth bit is set in i for k = 0 to n if j != k and kth bit is set in i and adj[k][j] == true if dp[k][ i XOR 2j ] == true
dp[j][i]=true break for i = 0 to n if dp[i][2n-1] == true return true return false
The next loop iterates over 0 to 2n-1, all the bitmasks, that means all the subsets of the vertices. And the loop inside it check which of the vertices from 0 to n-1 are present in subset S represented by a bitmask i. And the third loop inside it checks for every vertex j present in S, which of the vertices from 0 to n-1 are present in S and are neighbors of j. Then for every such vertex k it checks whether the cell dp[k][ i XOR 2j ] is true or not. What does this cell represents? In binary conversion of i XOR 2j every bit which is 1 in binary conversion of i remains 1 except the jth bit. So i XOR 2j represents the subset S-{j} and the cell dp[k][ i XOR 2j ] represents whether there is a path that visits each vertex in the subset S-{j} exactly once and ends at k. If there is a path that visits each vertex in S-{j} exactly once and ends at k than adding the edge k-j will extend that path to visit each vertex in S exactly once and end at j. So dp[j][i] will be true if there is such a path.
Finally there is a loop that iterates over all the vertices 0 to n-1 and checks if the cell dp[i][2n-1] is true or not, where 0 ≤ i < n. In the binary conversion of 2n-1 every bit is 1, that means it represents the set containing all the vertices and cell dp[i][2n-1] represents whether there is a path that visits every vertex exactly once and ends at i. If there is such a path it returns true i.e. there is a Hamiltonian path in the given graph. In the last line it returns false, that means no Hamiltonian path is found in the given graph. Following is the C++ implementation of the above method:
Here's how the table dp looks like for the graph given in Fig. 2 filled upto the mask 6.bool check_using_dp(int adj[][MAXN], int n){ bool dp[MAXN][1<<MAXN]={0}; for(int i=0; i<n; i++) dp[i][1<<i]=true; for(int i=0; i<(1<<n); i++){ for(int j=0; j<n; j++) if(i&(1<<j)){ for(int k=0; k<n; k++) if(i&(1<<k) && adj[k][j] && k!=j && dp[k][i^(1<<j)]){ dp[j][i]=true; break; } } } for(int i=0; i<n; i++) if(dp[i][(1<<n)-1]) return true; return false; }

Let's fill it for the mask 7 i.e. for the subset S={0, 1, 2}.
For cell dp[ 0 ][ 7 ], 0 has a neighbor in S i.e. 1, check if there is a path that visits each vertex in subset represented by 7 XOR 20 = 6 i.e. {1, 2}, exactly once and ends at 1, i.e. the cell dp[ 1 ][ 6 ]. It is true so dp[ 0 ][ 7 ] will also be true.
For cell dp[ 1 ][ 7 ], 1 has two neighbors in S i.e. 0, 2. So check for the bitmask 7 XOR 21 = 5 i.e. the subset {0, 2}. Here both the cells dp[ 0 ][ 5 ] and dp[ 2 ][ 5 ] are false. So the cell dp[ 1 ][ 7 ] will remain false.
For cell dp[ 2 ][ 7 ], 2 has a neighbor in S i.e. 1, check if there is a path that visits each vertex in subset represented by 7 XOR 22 = 3 i.e. {0, 1}, exactly once and ends at 1, i.e. the cell dp[ 1 ][ 3 ]. It is true so dp[ 2 ][ 7 ] will also be true.
For cell dp[ 3 ][ 7 ], clearly 3 {0, 1, 2}. So dp[ 3 ][ 7 ] will remain false.
Here's how the complete table will look like.

Now clearly the cells dp[ 0 ][ 15 ], dp[ 2 ][ 15 ], dp[ 3 ][ 15 ] are true so the graph contains a Hamiltonian Path.
Time complexity of the above algorithm is O(2nn2). - Depth first search and backtracking can also help to check whether a Hamiltonian path
exists in a graph or not. Simply apply depth first search starting
from every vertex v and do labeling of all the vertices. All the
vertices are labelled as either "IN STACK" or "NOT IN STACK". A vertex is
labelled "IN STACK" if it is visited but some of its adjacent
vertices are not yet visited and is labelled "NOT IN STACK" if it is
not visited.
If at any instant the number of vertices with label "IN STACK" is equal to the total number of vertices in the graph then a Hamiltonian Path exists in the graph.
Following image shows how this algorithm will work for graph shown in Fig. 2.
So, clearly the number of vertices having label IN_STACK is 4 in the last step, so the given graph contains a Hamiltonian Path. Now let's see how it will work for graph in Fig. 1
The above image shows how it will work when DFS is strated with vertex 1. So clearly, the number of vertices having label IN_STACK is not equal to 4 at any stage. That means there is no Hamiltonian Path that starts with 1. When DFS is applied starting from vertices 2, 3 and 4 same result will be obtained. So there is no Hamiltonian Path in the given graph.
Following is the C++ implementation:
Worst case complexity of using DFS and backtracking is O(N!).#define NOT_IN_STACK 0
#define IN_STACK 1 bool dfs(int v, bool adj[][MAXN], int label[MAXN], int instack_count, int n){ if(instack_count == n) return true; for(int i=0; i<n; i++) if(adj[v][i] && label[i] == NOT_IN_STACK){ label[i]=IN_STACK; if(dfs(i, adj, label, instack_count+1, n)) return true; label[i]=NOT_IN_STACK; } return false; } bool check_using_dfs(bool adj[][MAXN], int n){ int label[MAXN]; for(int i=0; i<n; i++) label[i]=NOT_IN_STACK; for(int i=0; i<n; i++){ label[i]=IN_STACK; if(dfs(i, adj, label, 1, n)) return true; label[i]=NOT_IN_STACK; } return false; }
Try solving the following problem using all the three methods.

