Flood fill algorithm helps in visiting each and every point in a given area. It determines the area connected to a given cell in a multi-dimensional array. Following are some famous implementations of flood fill algorithm:
Bucket Fill in Paint:
Clicking in an area with this tool selected fills that area with the selected color.
Solving a Maze:
Given a matrix with some starting point, and some destination with some obstacles in between, this algorithm helps to find out the path from source to destination
Minesweeper:
When a blank cell is discovered, this algorithm helps in revealing neighboring cells. This step is done recursively till cells having numbers are discovered.
Flood fill algorithm can be simply modeled as graph traversal problem, representing the given area as a matrix and considering every cell of that matrix as a vertex that is connected to points above it, below it, to right of it, and to left of it and in case of 8-connections, to the points at both diagonals also. For example, consider the image given below.
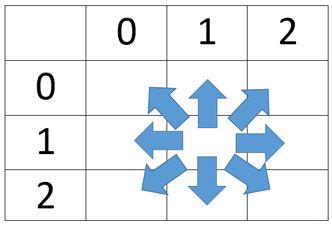
It clearly shows how the cell in the middle is connected to cells around it. For instance, there are 8-connections like there are in Minesweeper (clicking on any cell that turns out to be blank reveals 8 cells around it which contains a number or are blank). The cell (1,1) is connected to (0,0), (0,1), (0,2), (1,0), (1,2), (2,0), (2,1), (2,2).
In general any cell (x,y) is connected to (x−1,y−1), (x−1,y), (x−1,y+1), (x,y−1), (x,y+1), (x+1,y−1), (x+1,y), (x+1,y+1). Of course, the boundary conditions are to be kept in mind.
Now that the given area has been modeled as a graph, a DFS or BFS can be applied to traverse that graph. The pseudo code is given below.
function DFS(x, y, visited, n, m)
if (x ≥ n OR y ≥ m)
return
if(x < 0 OR y < 0)
return
if(visisted[x][y] == True)
return
visited[x][y] = True
DFS(x-1, y-1, visited, n, m)
DFS(x-1, y, visited, n, m)
DFS(x-1, y+1, visited, n, m)
DFS(x, y-1, visited, n, m)
DFS(x, y+1, visited, n, m)
DFS(x+1, y-1, visited, n, m)
DFS(x+1, y, visited, n, m)
DFS(x+1, y+1, visited, n, m)
The above code visits each and every cell of a matrix of size n×m starting with some source cell. Time Complexity of above algorithm is O(n×m).
One another use of flood algorithm is found in solving a maze. Given a matrix, a source cell, a destination cell, some cells which cannot be visited, and some valid moves, check if the destination cell can be reached from the source cell. Matrix given in the image below shows one such problem.
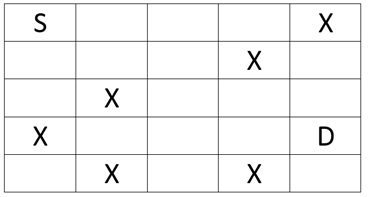
The source is cell (0,0) and the destination is cell (3,4). Cells containing X cannot be visited. Let's assume there are 4 valid moves - move up, move down, move left and move right.
Following pseudo code solve the problem given above.
function DFS(x, y, visited, n, m, mat, dest_x, dest_y)
if(x == dest_x AND y == dest_y)
return True
if(x ≥ n OR y ≥ m)
return False
if(x < 0 OR y < 0)
return False
if(visisted[x][y] == True)
return False
if(mat[x][y] == X)
return False
visited[x][y] = True
if (DFS(x+1, y, visited, n, m, mat, dest_x, dest_y) == True)
return True
if (DFS(x-1, y, visited, n, m, mat, dest_x, dest_y) == True)
return True
if (DFS(x, y+1, visited, n, m, mat, dest_x, dest_y) == True)
return True
if (DFS(x, y-1, visited, n, m, mat, dest_x, dest_y) == True)
return True
return FalseThe code given above is same as that given previously with slight changes. It takes three more parameters including the given matrix to check if the current cell is marked X or not and coordinates of destination cell (destx,desty). If the current cell is equal to destination cell it returns True, and consequently, all the previous calls in the stack returns True, because there is no use of visiting any cells further when it has been discovered that there is a path between source and destination cell.
So for the matrix given in image above the code returns True.
If, in the given matrix the cell (1,2) was also marked X, then the code would have returned False, as there would have been no path to reach from S to D in that case.

