Telecom towers are an integral part of the telecom network infrastructure. In fact they are the most expensive to build and the valuations are heavy. The newly started mobile company in Hacker Land built \(n\) towers to enhance the connectivity of their users. You can assume that the Cartesian coordinate system is used in Hacker Land and the location of \(i^{th}\) tower is given as \((x_i, y_i).\)
After the construction of the towers company realised that there are many call drops happening with the users. One identified reason for the frequent call drop was that the pair of towers which are at Euclidean distance \(d\) were causing destructive interference. To resolve the issue the company decided to destroy some towers such that no two towers are at \(d\) distance. You have to tell the minimum number of towers that the company need to destroy such that no two towers are at distance \(d.\)
Note: The Euclidean distance between points \((x_1, y_1) \text{ and } (x_2, y_2)\) is the length of the line segment connecting them, which is same as \(\sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}\)
Constraints:
- \(2 \le n \le 10^4 \)
- \(1 \le d \le 200\)
- \(1 \le x_i, y_i\le 200\)
- There are no two towers with same location.
Input Format:
The first line contains two space-separated integers \(n\) and \(d\) denoting the number telecom towers constructed initially and the distance which causes destructive interference respectively.
Next \(n\) lines contains two-space separated integers denoting the \(x_i \text{ and } y_i \text{ }-\) location of the towers.
Output Format:
Print a single lines denoting the minimum number of towers that should be destroyed such that no two towers are separated by distance \(d.\)
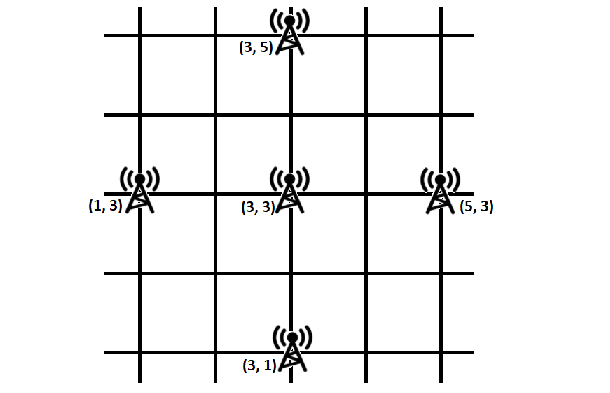
The image below shows the location of the towers, We can destroy the tower at \((3, 3).\)