Topological sorting of vertices of a Directed Acyclic Graph is an ordering of the vertices v1,v2,...vn in such a way, that if there is an edge directed towards vertex vj from vertex vi, then vi comes before vj. For example consider the graph given below:
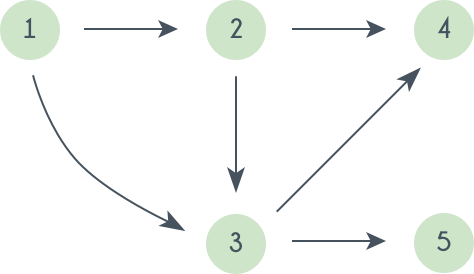
A topological sorting of this graph is: 1 2 3 4 5
There are multiple topological sorting possible for a graph. For the graph given above one another topological sorting is: 1 2 3 5 4
In order to have a topological sorting the graph must not contain any cycles. In order to prove it, let's assume there is a cycle made of the vertices v1,v2,v3...vn. That means there is a directed edge between vi and vi+1 (1≤i<n) and between vn and v1. So now, if we do topological sorting then vn must come before v1 because of the directed edge from vn to v1. Clearly, vi+1 will come after vi, because of the directed from vi to vi+1, that means v1 must come before vn. Well, clearly we've reached a contradiction, here. So topological sorting can be achieved for only directed and acyclic graphs.
Le'ts see how we can find a topological sorting in a graph. So basically we want to find a permutation of the vertices in which for every vertex vi, all the vertices vj having edges coming out and directed towards vi comes before vi. We'll maintain an array T that will denote our topological sorting. So, let's say for a graph having N vertices, we have an array in_degree[] of size N whose ith element tells the number of vertices which are not already inserted in T and there is an edge from them incident on vertex numbered i. We'll append vertices vi to the array T, and when we do that we'll decrease the value of in_degree[vj] by 1 for every edge from vi to vj. Doing this will mean that we have inserted one vertex having edge directed towards vj. So at any point we can insert only those vertices for which the value of in_degree[] is 0.
The algorithm using a BFS traversal is given below:
topological_sort(N, adj[N][N])
T = []
visited = []
in_degree = []
for i = 0 to N
in_degree[i] = visited[i] = 0
for i = 0 to N
for j = 0 to N
if adj[i][j] is TRUE
in_degree[j] = in_degree[j] + 1
for i = 0 to N
if in_degree[i] is 0
enqueue(Queue, i)
visited[i] = TRUE
while Queue is not Empty
vertex = get_front(Queue)
dequeue(Queue)
T.append(vertex)
for j = 0 to N
if adj[vertex][j] is TRUE and visited[j] is FALSE
in_degree[j] = in_degree[j] - 1
if in_degree[j] is 0
enqueue(Queue, j)
visited[j] = TRUE
return T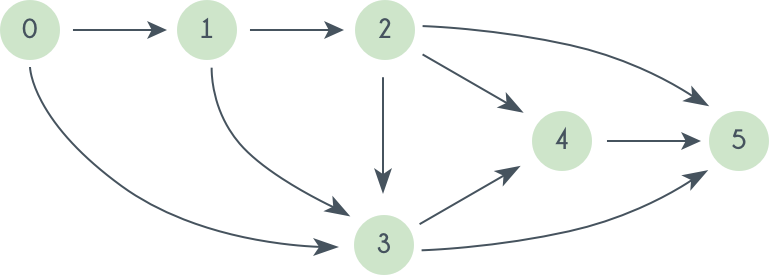
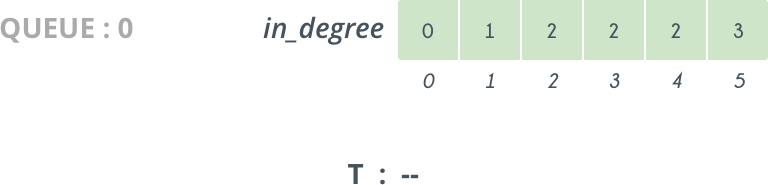
Initially in_degree[0]=0 and T is empty
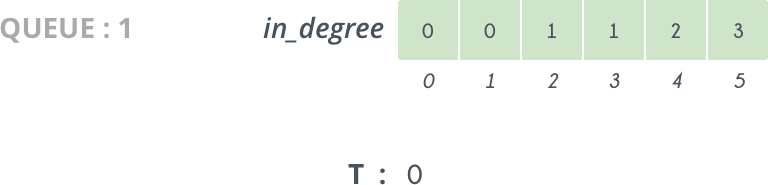
So, we delete 0 from Queue and append it to T. The vertices directly connected to 0 are 1 and 2 so we decrease their in_degree[] by 1. So, now in_degree[1]=0 and so 1 is pushed in Queue.
Next we delete 1 from Queue and append it to T. Doing this we decrease in_degree[2] by 1, and now it becomes 0 and 2 is pushed into Queue.

So, we continue doing like this, and further iterations looks like as follows:
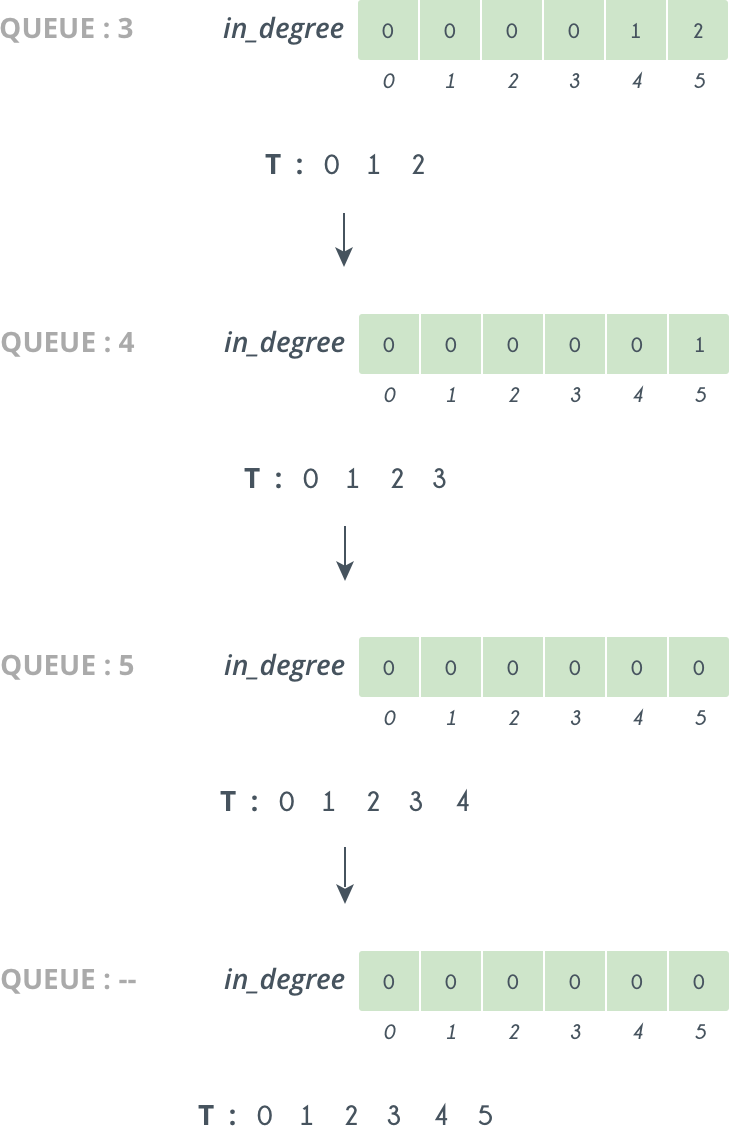
So at last we get our Topological sorting in T i.e. : 0, 1, 2, 3, 4, 5
Solution using a DFS traversal, unlike the one using BFS, does not need any special in_degree[] array. Following is the pseudo code of the DFS solution:
T = []
visited = []
topological_sort( cur_vert, N, adj[][] ){
visited[cur_vert] = true
for i = 0 to N
if adj[cur_vert][i] is true and visited[i] is false
topological_sort(i)
T.insert_in_beginning(cur_vert)
}


