Heap Sort
Heaps can be used in sorting an array. In max-heaps, maximum element will always be at the root. Heap Sort uses this property of heap to sort the array.
Consider an array Arr which is to be sorted using Heap Sort.
- Initially build a max heap of elements in Arr.
- The root element, that is Arr[1], will contain maximum element of Arr. After that, swap this element with the last element of Arr and heapify the max heap excluding the last element which is already in its correct position and then decrease the length of heap by one.
- Repeat the step 2, until all the elements are in their correct position.
Implementation:
void heap_sort(int Arr[ ])
{
int heap_size = N;
build_maxheap(Arr);
for(int i = N; i >= 2 ; i-- )
{
swap|(Arr[ 1 ], Arr[ i ]);
heap_size = heap_size - 1;
max_heapify(Arr, 1, heap_size);
}
}
Complexity:
max_heapify has complexity O(logN), build_maxheap has complexity O(N) and we run max_heapify N−1 times in heap_sort function, therefore complexity of heap_sort function is O(NlogN).
Example:
In the diagram below,initially there is an unsorted array Arr having 6 elements and then max-heap will be built.

After building max-heap, the elements in the array Arr will be:

Step 1: 8 is swapped with 5.
Step 2: 8 is disconnected from heap as 8 is in correct position now and.
Step 3: Max-heap is created and 7 is swapped with 3.
Step 4: 7 is disconnected from heap.
Step 5: Max heap is created and 5 is swapped with 1.
Step 6: 5 is disconnected from heap.
Step 7: Max heap is created and 4 is swapped with 3.
Step 8: 4 is disconnected from heap.
Step 9: Max heap is created and 3 is swapped with 1.
Step 10: 3 is disconnected.
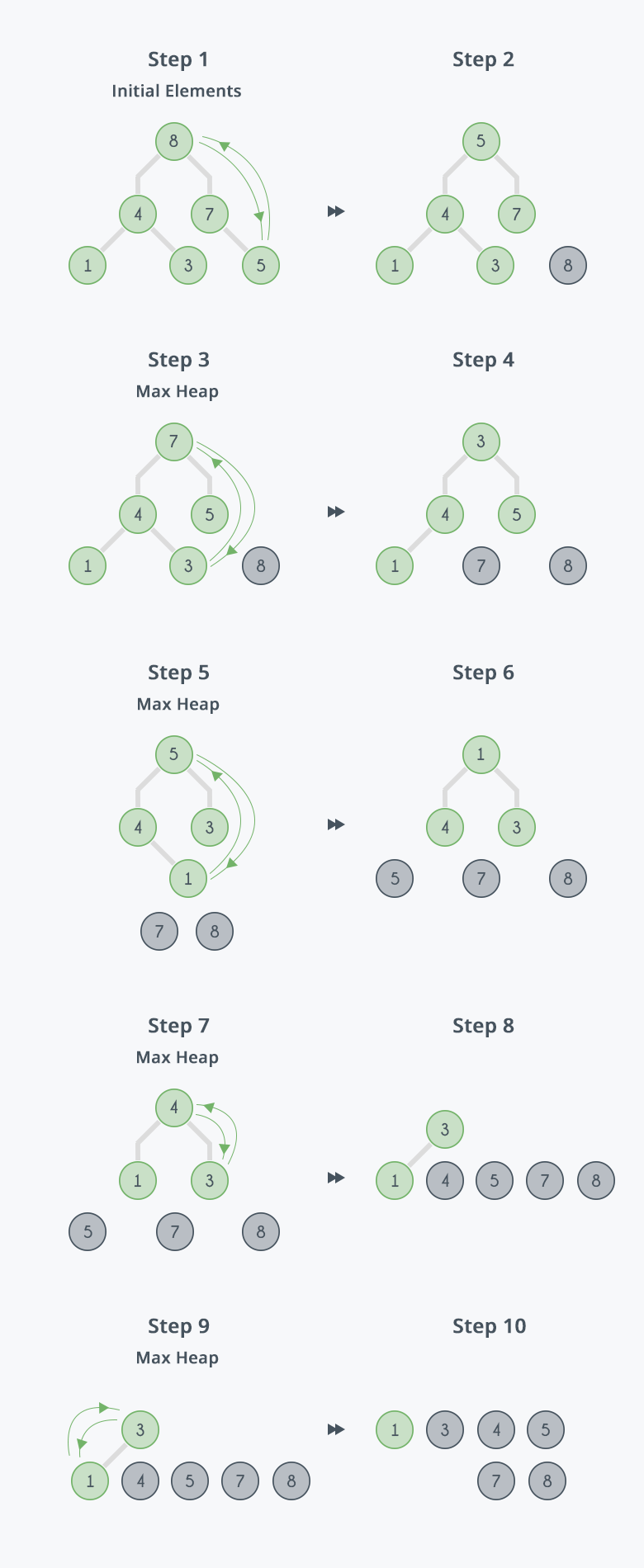
After all the steps, we will get a sorted array.


