Prerequisites : Depth-first-search(DFS)
If you aren't familiar with Graph, consider reading this article by Prateek Garg:
here
Hey, so if you are familiar with Graph theory, I'm sure you've come across the term Articulation point. So, before understanding what exactly AP(Articulation point ) is, first let me give you a motivation , on why do even study APs.
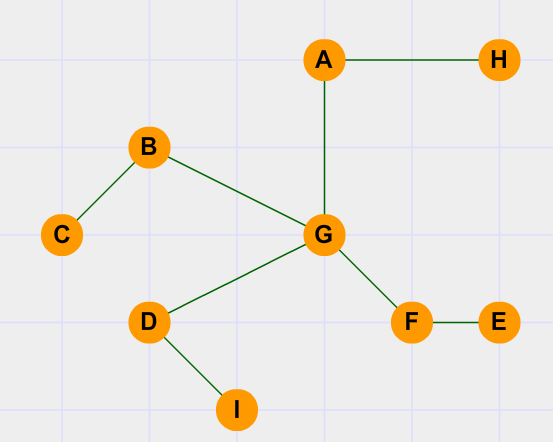
Okay, let us consider the situation of a war(yes a war!).In your country, there is a network of telephone lines between 9 cities(A,B,C...H,I) i.e. the 9 cities are connected by telephone line,(as shown in the figure above) which means that a message from one city to any other city can be transmitted through the line. Like we can transfer message from city A to city B even though they are not "directly" connected by a line.So what's the catch, everything seems fine, right?
Here it is: You are the "army-general" of your country and you've to take a decision, you have to find the city which,if damaged would incur the greatest network blockage (Considering that damaging the city damages all the connected telephone lines in it).
Take a moment and think...
Which city would you try to protect the most and why....?
Is G your answer , then "Yes" you're right, and WHY.
Because, a damage to city G will casue a "lot of network-flow to STOP".
Well that means, you no longer will be able to transfer message from city A to city B, (that's really hell of a trouble during a war time!!).
Now YOUR concern would be to identify such "vulnerable " points and send reinforcements to them..
A few terms I would use in my tutorial are:
1. Level: It is the distance from root of the graph, the root is said to be at level 0 and level increases as we go down the tree
2. DFS: It's the short for Depth-First-Search
3. AP: Short for Articulation Point or Cut-Vertex
3. Back-edge: You will know about it in a moment
......................................................................................................................
Let me give a more formal definition of AP:
A point in a graph is called an Articulation Point or Cut-Vertex if upon removing that point let's say P, there is atleast one child(C) of it(P) , that is disconnected from the whole graph.In other words at least one of P's child C cannot find a "back edge".
A what?. Okay let me explain it.
An edge , which connects a vertex to another vertex which has a *lower level,* is called a back-edge.
Our whole idea of finding APs rests on finding whether a node has a back edge or not, and even if it has a back edge does it take it to a lower level than the parent or NOT.
There are two ways in which a node can go for a back-edge:
1. Directly connect to a Node upper than it's parent's node like this:

B is having a back-edge to A (upper than it's parent C).
OR
2.. Indirectly by having such a child which has a back-edge,.
In the same figure, see that we're able to see that vertex C, which is the parent of B , has a back-edge because B has a back-edge to A!.
In simple words if a child has a back-edge its immediate parent definitely has it.
// And so, this is how we are going to deal with this. We are going to use a DFS algorithm to solve this
// question.
Code:
;
long MAXX 100007
void ini()
{
int i;
for(i =0;i<MAXX;i++)
{
vis[i]=AP[i]=false; // Initializing AP and vis array as false
parent[i]=-1; // Initializing parent of each vertex to -1
adj[i].clear(); // clearing the adjacency list.
low[i]=0;
}
tim=0; // initializing tim to 0
}
void dfs(int u)
{
vis[u]=true;
int i;
low[u]=disc[u]=(++tim);
int child=0;
for(i=0;i<adj[u].size();i++)
{
int v=adj[u][i];
if(vis[v]==false)
{
child++;
parent[v]=u;
dfs(v);
low[u]=min(low[u],low[v]);
if( (parent[u]!=-1) and ( low[v]>=disc[u] ) )
AP[u]=true;
if( (parent[u]==-1) and (child>1))
AP[u]=true;
}
else if(v!=parent[u])
{low[u]=min(low[u],disc[v]);}
}
}
If things doesn't make any sense right now, you can consider yourself an absolutely normal person..
First we see five arrays: vis[], low[] ,disc[], and AP[], parent[]
vis[ ]:
for making sure, if we have visited a node(a vertex) or not and not running into an
infinite loop .You can understand what I'm saying if you did the DFS.
AP[ ]:
it is a boolean array to mark if a vertex is Cut-vertex (or Articulation Point)
parent[ ]:
It keeps the record of parent of each vertex
Now read very carefully because, the low[ ] and disc[ ] array are the most important ones, and
play very significant roles in the detemination of APs.
disc[ ]:
It answers a simple question, when was a particular vertex " discovered"
in the depth- first-search ?, which means it assigns a number to the the vertex in the order it is found in the dfs. Why do we use it?, we'll see that later.
low[ x ]:
It answers yet another simple question, "what is lowest level vertex ,x can climb to, in case its parent is removed from the graph"
Be patient and try to grasp what they mean, as they are the most important aspect...
Now that we know what each array does (though we don't know why having them helps solve our problem ).let's examine the code
Code:
This snippet:
void dfs(int u)
{
vis[u]=true; // marks the current vertex as visited ,the usual DFS stuff
int i;
low[u]=disc[u]=(++tim); // for the current vertex allotes them an equal value tim and increments it .
int child=0; // It is has yet another story we will discover later
Notice that tim increases by one in each DFS call
Now here comes the recursion part:
Code:
for(i=0;i<adj[u].size();i++)
{
int v=adj[u][i];
if(vis[v]==false)
{
child++;
parent[v]=u;
dfs(v);
low[u]=min(low[u],low[v]);
if( (parent[u]!=-1) and ( low[v]>=disc[u] ) )
AP[u]=true;
if( (parent[u]==-1) and (child>1))
AP[u]=true;
}
else if(v!=parent[u])
{low[u]=min(low[u],disc[v]);}
}
.................................................................................................................................................................................
First let's see the else if part ( I'm doing this on purpose).
else if(v!=parent[u])
{low[u]=min(low[u],disc[v]);}u then we will find low[u] as
low[u]=min(low[u],dis[v]) // importnant piece of code Just sit back and watch :
Consider the situation given in the figure :

min(low[u],disc[v]) I hope this part is clear.
.................................................................................................................................................................................
Now let's check out the if-part
Code:
;
if(vis[v]==false)
{
child++; //Increments the value of child
parent[v]=u; // Keeps track of parent of each vertex
dfs(v); // Recursive call to DFS
low[u]=min(low[u],low[v]);
if( (parent[u]!=-1) and ( low[v]>=disc[u] ) )
AP[u]=true;
if( (parent[u]==-1) and (child>1))
AP[u]=true;
}
Output:
Err... you must be thinking "What's the rest part of code for (after dfs(v)), I mean
will they ever get executed?". Actually I had this confusion because of lack of knowledge of recursion. Remember the "stack-thing", they told about recursion, "Last-In-First-Out". Yeah, that's it. They will get executed when the recursion starts the popping execution. Let's have a look.

Let A be our root node
DFSA => DFSB => DFSC => DFSD =>(no more dfs because D is the leaf node in the graph),
So it will pop from the recursion stack and we will have another child of C on the stack
i.e. E
DFSA => DFSB => DFSC => DFSD =>(pop)
DFSA => DFSB => DFSC => DFSE =>(pop)
DFSA => DFSB => DFS3(pop)
DFSA => DFSB =>(pop)
DFSA => DFSF=>(pop)
DFSA
So when DFSD ends the "rest part" of DFSC continues..
It assigns
low[u]= min(low[u],low[v]);Aha.. While you might be thinking ,that low[u] should always be less than low[v] , rethinnk.. Remember what we did in the "else-if" part. Yeah, correct!!
In cases when there are back-edges these CAN happen
But why do we DO `low[u]=min(low[u],low[v])` It's simply because "if the child has a back-edge, so will its immediate parent",remember that?
Then notice what we did in the very next line,
if( (parent[u]!=-1) and ( low[v]>=disc[u] ) )
AP[u]=true;It says that if parent[u]!=-1 meaning that it is NOT the root node, and low[v]>=disc[u] which means there is no back edge of the child "v" of "u" , or even "if it has a back-edge it is upto u only ,(in case when low[ v]= disc[u])", so the point u is eligible to be the AP.
Phew.. finally , we have 85% of our work done.. Wait what are we missing, Oh yeah that "child"
variable mystery I promised to tell you.
Checking if the root is an AP or not.
-------------------------------------Me: When can a root be an Articulation point,
You: Always if it has 2 or more child?
Me: NOOO STOP right there.
This is a terrible mistake we generally do.
A root node is NOT necessarily an articulation point if it has >=2 children
Consider the case:

If A is the root node , and it has two child nodes, but it is obviously NOT an articulation point.So what this "child-variable" counts is NOT the no of children of the root, but the no of subtree of Root.
if( (parent[u]==-1) and (child>1)) // checks if u is the root node or not and child>1
AP[u]=true; Solve this question on LightOj , named Ant Hills:
here
