Given a tree with N nodes and N−1 bidirectional edges, and given an integer S. Now, you have to assign the weights to the edges of this tree such that:
1. the sum of the weights of all the edges is equal to S
2. for every possible diameter of the tree, the maximum weight over all the edges covered by its path is the minimum possible
You have to output this minimum possible edge weight.
Note: The diameter of a tree is the number of nodes on the longest path between two leaves in the tree.
Input Format
The first line of the input contains an integer T, the total number of test cases.
The first line of each test case contains two space-separated integers N and S, the number of nodes in a tree and the integer S as mentioned in the problem statement.
Then the N−1 lines follow, each containing two space-separated integers u and v representing that there is a bidirectional edge between the nodes u and v.
Output Format
For each test case output the minimum possible edge weight which satisfies the above-mentioned conditions.
Constraints
1≤T≤10
1≤N≤2×103
1≤u,v≤N
1≤S≤109
Sample test case 1: Given below is one of the best ways to assign weights to the edges
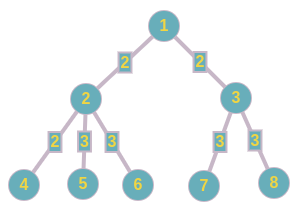
Sample test case 2: Note that there are only two possible diameters of the tree: 5 to 7 and 6 to 7 , so we can assign S to the edge {1,4} and for every possible diameter of the tree, the maximum weight over all the edges covered by its path is 0


