You are given a rooted tree with N nodes. Each node has a value Val[node], associated with it and there is a monkey on each one of the nodes.
Every monkey can only climb up the tree as long as the value of the node he encounters is different from all the previous values.
Consider a pair of monkeys on nodes U and V. We say that such a pair is good if the distance between U and V is K and the monkeys can possibly meet.
You need to find the expected value of the number of good pairs amongst all the monkeys on a random simple path chosen in the tree.
The expected value can be represented in the form P/Q where P and Q are coprime integers. Output PQ−1%1000000007
Note
- Monkeys can only climb up.
- Root of the tree is node 1.
- Distance between a pair of nodes (U,V) is the number of edges on the simple path from U to V.
- The pairs are unordered.
Input Format
- The First line contains integers N and K.
- Next line contains N−1 space seperated integers where the ith one represents the parent of (i+1)th node.
- Next line contains N space seperated integers where ith of them represents Val[i], the value of the ith node.
Output Format
- Print a single integer representing the expected value as asked.
Constraints
- 1≤K≤N≤105
- 1≤Val[i]≤105
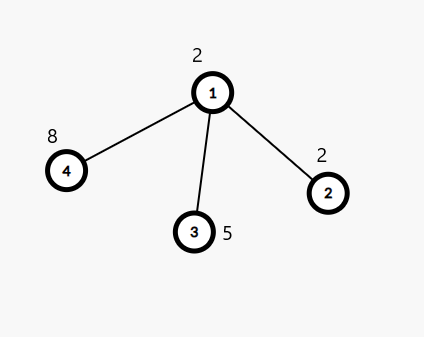
The monkey at nodes 3 and 4 can reach upto 1 while the monkey at node 2 can not climb up at all.
Let us consider all paths one by one.
Path 1−2, 1−3 and 1−4 does not contain any pair which is 2 units apart. Hence no good pair on them.
Path 2−3. contains the pair (2,3) which is 2 units apart but they do not form a good pair as they can not meet.
Path 2−4. contains the pair (2,4) which is 2 units apart but they do not form a good pair as they can not meet.
Path 4−3. contains the pair (4,3) which is 2 units apart and they do form a good pair as they can meet.
So, answer is 1/6=166666668%1000000007

