The concept of magnitude or absolute value is generalized to the concepts of norms for vectors and matrices. Given an n-dimensional vector

a general vector norm, denoted by ‖x‖, is a nonnegative norm defined such that:

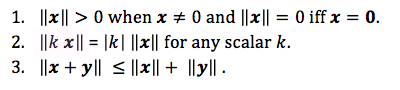
Vector norms which are instances of p-norms, where p is an integer, p>0, for an n-vector x, is defined by

Important cases are:

1-norm:

sometimes called the Manhattan norm because in the plane it corresponds to the distance between two points as measured in “city blocks”.

2-norm:

which correspond to the usual notion of distance in Euclidean space, hence this is called the Euclidean norm.

∞-norm:

which can be viewed as a limiting case as p→∞.

For the vector

Your task is to compute the 1-,2-, and ∞-norm, given an n-vector x.

INPUT

Input consists of several lines. Each line consists a positive integer n, $1 \le n \le 1000$, followed by n real numbers representing the elements of the vector in the transposed form. Each element is separated by a single space.

OUTPUT

Output consists of several lines correspond to each line in the input. Each line in the output must consists three real numbers namely the 1-, 2- and ∞-norm of the vector rounded to six (6) decimal places. Each number must be separated by a single space.

SAMPLE INPUT

2 -1.6 1.2
3 1 2 3

SAMPLE OUTPUT

2.800000 2.000000 1.600000
6.000000 3.741657 3.000000